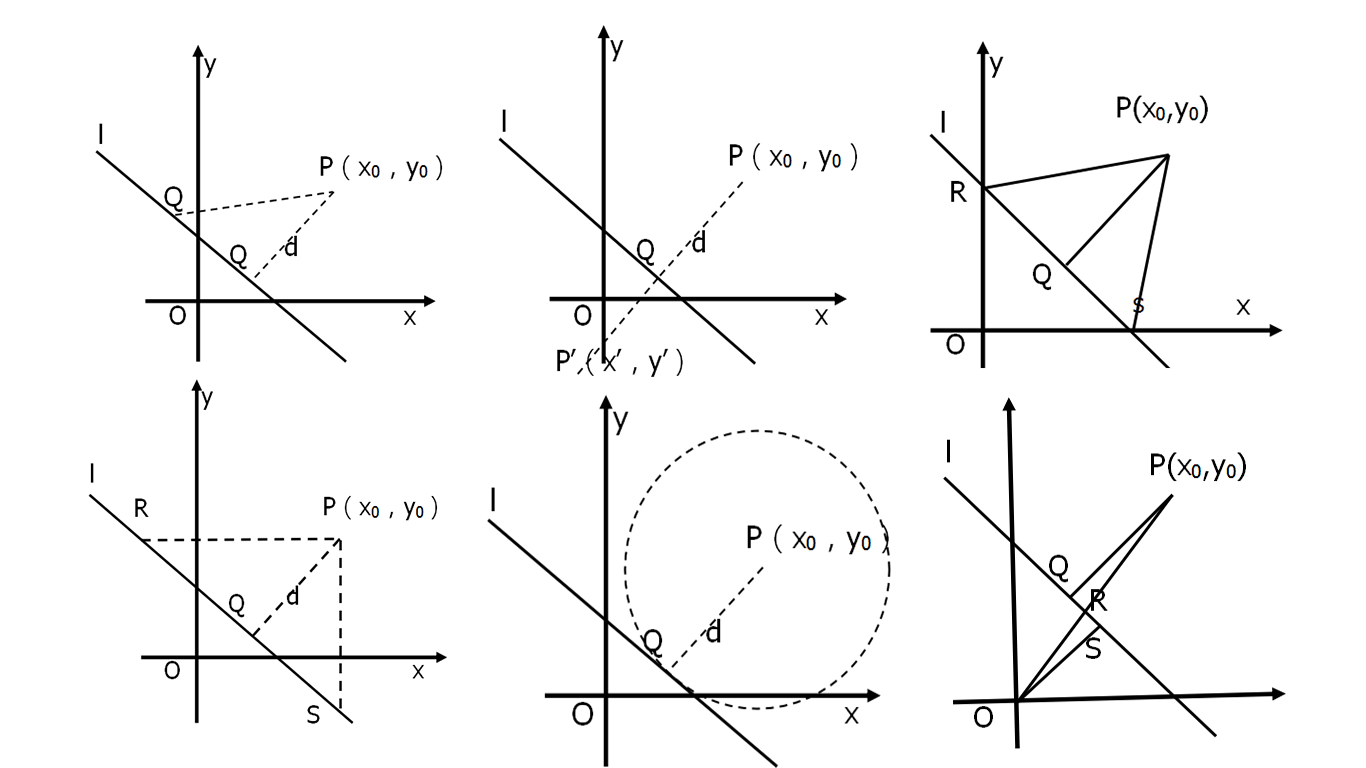
点到直线距离公式的几种推导

摘要：本文将介绍几种推导点到直线的距离公式的方法。

本文默认情况下，直线的方程为l:Ax+By+C=0，A，B均不为0，斜率为k_l，点的坐标为P(x0，y0)，点P到l的距离为d。

推导一（面积法）：

如上图所示，设R(x_R,y_0)，S(x_0,y_S)，由R，S在直线l上，得到：

Ax_R+By_0+C=0，

Ax_0+By_S+C=0，

所以：x_1 = \frac{-By_0-C}{A}，y_2 = \frac{-Ax_0-C}{B}，

所以：|PR|=|x_0-x_1|=\left | \frac{Ax_0+By_0+C}{A} \right |，|PS|=|y_0-y_2|=\left | \frac{Ax_0+By_0+C}{B} \right |，

于是：|RS| = \sqrt{|PR|^2+|PS|^2} = \frac{\sqrt{A^2+B^2} }{AB} \cdot |Ax_0+By_0+C|，

所以从三角形面积公式知：d\cdot |RS|=|PR|\cdot |PS|，

从而有：d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导二（三角函数斜率法）：

如上图所示，直线的倾角为α，同推导一，|PR|=|x_0-x_1|=\left | \frac{Ax_0+By_0+C}{A} \right |，

d = ||PR|sin\angle PRQ|=||PR|sin \alpha |，

又有|tan\alpha |=|k_l|=\left | \frac{A}{B} \right |及三角函数公式\frac{1}{tan^2\alpha } = \frac{1}{sin^2\alpha } - 1，

代入消去α，便有：d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导三（求点法）：

如上图所示：因为k_{PQ}\cdot k_l=-1，所以k_{PQ}=\frac{B}{A}，

所以直线PQ方程为：y-y_0=\frac{B}{A}(x-x_0)，

联立Ax+By+C=0，

求出Q点的坐标为Q(\frac{B^2x_0-ABy_0-AC}{A^2+B^2},\frac{A^2y_0-ABx_0-BC}{A^2+B^2})，

所以：d=|PQ|=\sqrt{(\frac{B^2x_0-ABy_0-AC}{A^2+B^2} - x_0)^2+(\frac{A^2y_0-ABx_0-BC}{A^2+B^2}-y_0)^2}

=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导四（造圆切线法）：

如上图所示，以点P为圆心，作圆与直线l相切，则此圆的方程为：

(x-x_0)^2+(y-y_0)^2=d^2，

联立直线方程Ax+By+C=0消去y得：

(\frac{A^2}{B^2}+1)x^2+(\frac{2AC}{B^2}+\frac{2A}{B}y_0-2x_0)x + (x_0^2+y_0^2+\frac{C^2}{B^2}+\frac{2Cy_0}{B}-d^2) = 0，

由相切的条件知：\Delta =0，

即：(\frac{2AC}{B^2}+\frac{2A}{B}y_0-2x_0)^2-4\cdot (\frac{A^2}{B^2}+1)\cdot (x_0^2+y_0^2+\frac{C^2}{B^2}+\frac{2Cy_0}{B}-d^2) = 0，

解得：d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导五（函数极值法）：

如上图所示，该问题可以转化为求直线l上一动点Q，使得PQ的距离最短，当然我们已经知道d是最短的，这样，问题就变为了一个二元函数的条件极值问题，函数为：|PQ|=d(x,y)=\sqrt{(x-x_0)^2+(y-y_0)^2} ，d就是函数，条件就是Ax+By+C=0，求最小值，由于距离始终大于0，我们考虑根号里面的二元二次函数极值问题，我们采用拉格朗日乘数法。

令L(x,y,\lambda )=(x-x_0)^2+(y-y_0)^2+\lambda (Ax+By+C)，

所以\left\{\begin{aligned}&L_x'= 2(x-x_0)+\lambda A = 0 & \\ &L_y' = 2(y-y_0)+ \lambda B & \\&L_\lambda ' = Ax+By+C = 0 & \end{aligned}\right.，

解得：x=\frac{B^2x_0-ABy_0-AC}{A^2+B^2}，y = \frac{A^2x_0-ABx_0-BC}{A^2+B^2}。

代入函数中，即得：d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导六（对称求点法）：

如上图所示，设P(x',y')是P(x_0,y_0)关于直线l的对称点，于是有：

\left\{\begin{aligned}&\frac{y'-y_0}{x'-x_0} \cdot (-\frac{A}{B}) = -1 & \\&A\cdot \frac{x'+x_0}{2} + B\cdot \frac{y'+y_0}{2} + C = 0 & \end{aligned}\right.，

解得：x'=\frac{B^2x_0-ABy_0-AC}{A^2+B^2}-x_0，y' = \frac{A^2x_0-ABx_0-BC}{A^2+B^2} - y_0，

所以：d=\frac{1}{2}\sqrt{|PP'|^2} =\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导七（求高法）：

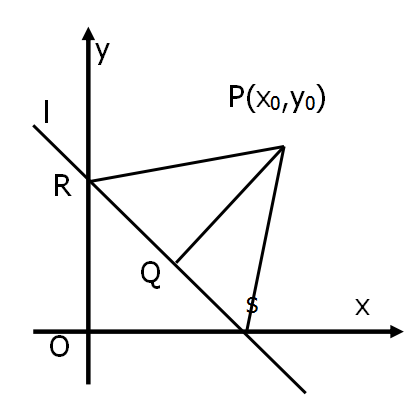
如上图所示，由直线方程可求得R、S的坐标，即R(0,-\frac{C}{B})，S(-\frac{C}{A},0)，于是三角形ROS的面积为：S_{\triangle ROS} = \left | \frac{1}{2}\begin{vmatrix} -x_0 & -\frac{C}{B}-y_0 \\-\frac{C}{A}-x_0 & -y_0 \end{vmatrix} \right |，

所以：|RS| = \sqrt{(\frac{C}{A})^2+(\frac{C}{B})^2} =\left | \frac{C\sqrt{A^2+B^2} }{AB} \right |，

所以：d=\frac{2S_{\triangle ROS}}{|RS|}=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

推导八（相似三角形法）：

如图所示，PQ\bot l，OS\bot l，于是\triangle PRS\sim \triangle ORQ，于是\frac{d}{|OS|}=\frac{|PR|}{|OR|} = \lambda ，

由直线分线段比公式（定比分点公式及定理）可得：\lambda = \frac{Ax_0+By_0+C}{|C|}，

而|OS| = \frac{\frac{C}{A}\cdot \frac{C}{B}}{|\frac{C\sqrt{A^2+B^2} }{AB}|} = \frac{|C|}{\sqrt{A^2+B^2}}，

所以d=\lambda |OS|=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2} }。

总结：平面解析几何主要的研究对象是直线与圆锥曲线，而平面几何主要的对象是直线以及由线段组成的几何图形，因此在解析几何的问题中，往往使用平面几何的知识就能带来更加简洁的过程，同时，我们可以发现，即便是一个简单的问题，也会有许多不同的办法，每一种办法都是一个知识点的应用，善于发现并比较这些方法，会更让我们的思维开阔，创新就是这么来的！